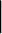 dz
dz be a Hermitian pseudo-metric on
Dr,
h∈C2(Dr), with ω the associated
(1, 1)-form. If
Ric
be a Hermitian pseudo-metric on
Dr,
h∈C2(Dr), with ω the associated
(1, 1)-form. If
Ric  ω≥ω on
Dr,
then
ω≤ωr on all of
Dr (or equivalently,
ds2≤dsr2).
ω≥ω on
Dr,
then
ω≤ωr on all of
Dr (or equivalently,
ds2≤dsr2).This is a repeat of the first section but with numbers in theorem heads swapped to the left.
Ahlfors' Lemma gives the principal criterion for obtaining lower bounds on the Kobayashi metric.
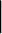 dz
dz be a Hermitian pseudo-metric on
Dr,
h∈C2(Dr), with ω the associated
(1, 1)-form. If
Ric
be a Hermitian pseudo-metric on
Dr,
h∈C2(Dr), with ω the associated
(1, 1)-form. If
Ric  ω≥ω on
Dr,
then
ω≤ωr on all of
Dr (or equivalently,
ds2≤dsr2).
ω≥ω on
Dr,
then
ω≤ωr on all of
Dr (or equivalently,
ds2≤dsr2).
Then our main theorem:
![[*]](crossref.png) ) holds.
) holds.